تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر


شاپا پرینت: 0733-9445 وبسایت مرجع 30 رفرنس دارد
18,400 تومانشناسه فایل: 9923
- حجم فایل ورد: 377.7KB حجم پیدیاف: 71.1KB
- فرمت: فایل Word قابل ویرایش و پرینت (DOCx)
- تعداد صفحات فارسی: 17 انگلیسی: 8
- دانشگاه:Professor, Dept. of Civil Engineering, Indian Inst. of Technology Kanpur, Kanpur 208 016, India
- ژورنال: Journal of Structural Engineering (1)
مقدمه مقاله
ساختمانها به ندرت اگر اصلا وجود داشته باشند، کاملا متقارن هستند و نوسانات ساختمانی به طور مکرر شامل اتصال جنبش جانبی و پیچشی (اتصال پیچشی) میشود. علاوه بر گریز از مرکز استاتیک (esj) [تعریف شده به صورت مسافت بین مرکز جرم (CM) و مرکز صلبیت (CR) در طبقات مربوطه]، قوانین اغلب مستلزم این هستند که طراح گریز از مرکز تصادفی را شامل نماید. یک گریز از مرکز تصادفی عواملی مثل مولفه ی چرخشی حرکت زمین حول محور عمودی، اختلاف بین مقادیر محاسبه شده و واقعی جرم، صلبیت یا تاب ارتجاعی و یک توزیع نامطلوب جرم بار زنده را تخمین میزند. مقررات قانونی در زمینه ی پیچش، به طور قابل توجهی متفاوت هستند. در عین حال، این مقررات در اکثر قوانین برای طراحی گریز از مرکز edj در طبقه ی jام برای آنالیز استاتیک ساختمانها میتواند به صورت شکل کلی زیر بیان شود:

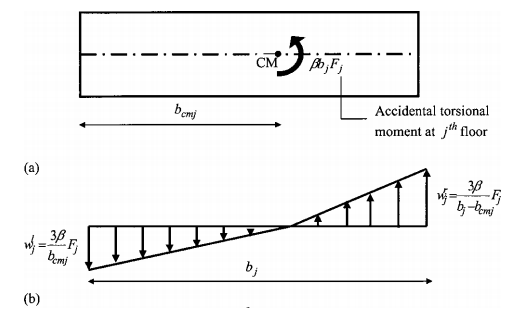
در این رابطه esj= گریز از مرکز استاتیک در طبقه ی jام؛ bj= بعد پلان طبقه ی jام نرمال برای جهت جنبش زمین؛ α،β و δ، ثابتهای ویژه هستند. برای نمونه طبق UBC (1997) و NEHRP (1997 a,b) α=1.0, β=0.05, and δ=1.0 ؛ طبق NZS 4203 (1992) α=1.0, β=0.1, and δ=1.0؛ طبق NBCC (1995) α=1.5, β=0.1, and δ=0.5؛ طبق MCBC (1995) α=1.5, β=0.1, and δ=1.0. در معادلات 1 الف و 1ب، عبارت اول سمت راست، اثر پیچشی جانبی متصل را محاسبه میکند که از عدم تقارن هم چنین تقویت به خاطر اثرات دینامیکی پدید می آید در حالیکه عبارت دوم اثر پیچشی تصادفی را بهمراه دارد. واکنش حاصل از معادلات 1الف و 1ب هر چه بالاتر باشد، باید در این طراحی بکار رود.
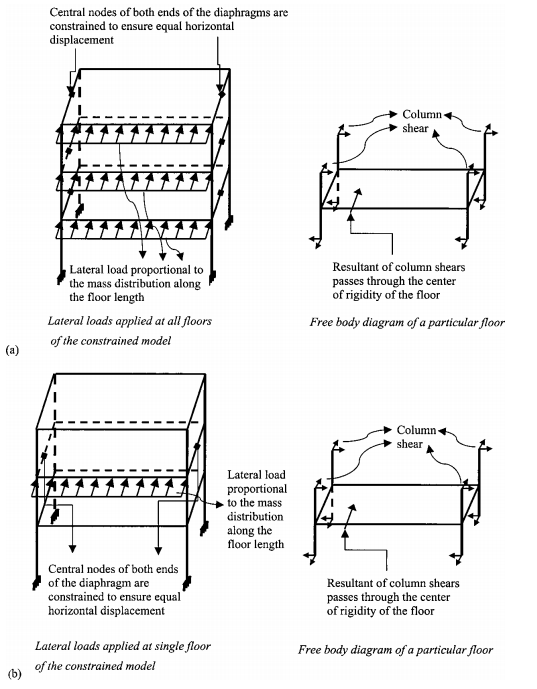
هرجا قوانین ساختمان α=δ=1.0 (مثلا در UBC 1997؛ NZS 4203 ، 1992) را مشخص کنند، موقعیت مکانی CR نیاز به محاسبه ی صریح ندارد تا مقررات پیچشی را اجرا نماید. در چنین مواردی، یک ساختمان دیافراگم طبقه ای صلب میتواند با بکارگیری نیروی جانبی طراحی در یک نقطه ی دور از CM با +Bbj یا –Bbj بسته به مورد، مورد تحلیل قرار گیرد. در عین حال، در جاییکه قوانین مقادیر α و δ متفاوت از 1.0 را مشخص میکنند (مثلا در 1995 NBCC؛ 1995 MCBC)، عقیده ی کلی بکار رفته این است که نیاز است CR مکان یابی شود. مشکلاتی در محاسبه ی صریح موقعیت مکانی CR در یک شیوه ی ساده وجود دارد. هجال و کوپرا (1987) یک ماتریس صلبیت بر مبنای فرمولاسیون مکان یابی CR و رویکرد قابل اجرا برای دیافراگم به شکل اختیاری با جهت گیری اختیاری صفحات اصلی عناصر مقاومت کننده بار جانبی را ارائه کرده اند. در عین حال، این رویکرد به ساختمانهای دارای دیافراگم های طبقه ای صلب محدود است و نمیتواند با نرم افزار آنالیز ساختمان استاندارد در دسترس اجرا شود. در حدود همان زمان، یک روش مشابه، توسط الکوسر (1986) و دامی –ریوس و الکوسر (1987) اثبات شد. یک رویکرد مبتنی بر انطباق (گوئل و کوپرا 1993) برای اجرای معادله 1 مطرح شد، که نیازی به موقعیت یابی CR به طور صریح ندارد. در عین حال، این رویکرد فقط برای ساختمانهای با دیافراگم های طبقه ای صلب قابل اجراست که دارای سیستم قائم هستند.
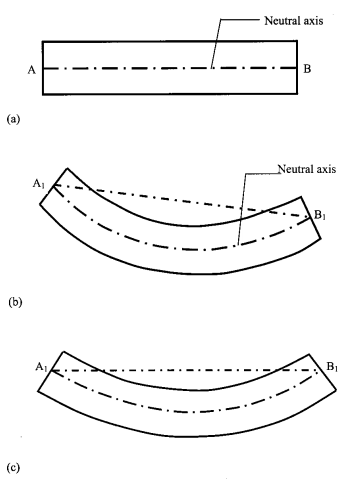
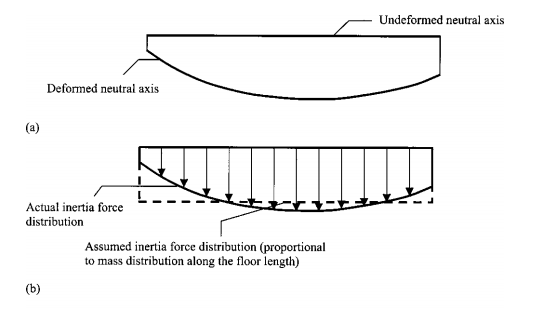
یک دیافراگم طبقه ای صلب یک فرضیه مناسب در اکثر ساختمانهاست. در عین حال، دیافراگمهای طبقه در برخی ساختمانها ممکن است دارای انعطاف پذیری قابل ملاحظه ای در صفحه ی خود باشند (مثلا ساختمانهایی که طویل و باریک اند یا ساختمانهایی که دارای دیوارهای انتهایی سفت هستند. در چنین ساختمانهایی، طراحی نیرو برای یک طبقه ی خاص نمیتواند در یک نقطه ی واحد (مثلا، CM یا در برخی خروج از مرکزیتها) از آن طبقه اعمال شود. اگر صفحات بتنی طبقه، کاملا انعطاف پذیر باشند، توزیع بار جانبی با مفهوم جرم انشعابی کنترل میشود و مساله ی پیچش در تصویر وارد نمیشود. در عین حال، تاوه های کف، دارای انعطاف پذیری متوسط هستند، یعنی دیافراگم های طبقه ای که نه صلب هستند و نه کاملا انعطاف پذیرند، انعطاف پذیری دیافراگم طبقه ای باید به طور صریحی در این آنالیز محاسبه شود. یک میزان قابل توجه از آثار در زمینه ی پویایی ساختمانهای دارای دیافراگم های طبقه ای انعطاف پذیر در دسترس هستند (مثلا شِپرد و دونالد 1967؛ جین و جنینگز 1984؛ جین 1984 الف وب؛ لیو و همکارانش 1984؛ جین و جنینگز 1985؛ کلبی و همکارانش، 1989؛ جین و ماندال 1992؛ تنا- کولانگا 1992؛ جین و ماندرال 1995؛ تنا- کالانگا و ابرامز 1995، 1996؛ تریمبلی و استمر 1996؛ مدهکار 1997؛ دی لا کالینا 1999؛ جو و لین 1999؛ تریمبلی و همکارانش 2000). در عین حال تنها تعداد محدودی از آثار منتشره در زمینه ی آنالیز دینامیکی ساختمانهای دیافراگم طبقه ای نامتقارن میتوانند موقعیت یابی شوند (مثلا تنا- کالانگا 1992؛ تنا- کالانگا و ابرامز 1995، 1996؛ دی لا کالینا 1999). به علاوه، آنالیز زلزله ی استاتیک ساختمانهای نامتقارن با دیافراگم های طبقه ای انعطاف پذیر، هنوز در آثار مورد بررسی قرار نگرفته است. به علاوه، مفهوم CR برای سیستم طبقه ی انعطاف پذیر، نیاز به فرموله شدن دارد.
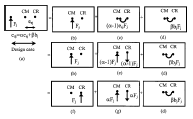
این مقاله، راه کاری برای آنالیز زلزله ی استاتیک ساختمانهای دارای انعطاف پذیری دیافراگم طبقه ای قابل توجه (اما نه کاملا انعطاف پذیر) هم چنین اتصال پیچشی را ارائه میدهد. رویکرد ارائه شده توسط گوئل و کوپرا (1993)برای سیستم طبقه صلب اصلاح شده است و به طور مناسبی به ساختمانهای دارای دیافراگم های طبقه ای انعطاف پذیر گسترش یافته اند. دو تعریف مرکز صلبیت، به نام کل طبقات و تک طبقه برای ساختمانهای دارای دیافراگم های طبقه انعطاف پذیر ارائه میشوند. روش ارائه شده، به گونه ای است که هرچه سختی دیافراگم زیاد شود، نتایج به موارد قابل اجرا برای ساختمانهای دارای دیافراگم های طبقه سخت نزدیکتر میشوند.
فرض میشود ساختمان فقط دارای یک جناح واحد باشد (مثلا مستطیلی یا ذوزنقه ای در پلان) و ساختمانهای دارای جناح های متعدد (مثلا به شکل L, V, Y, و غیره ) در نظر گرفته نشوند. در عین حال، عناصر مقاومت کننده در برابر بار جانبی نیاز ندارند به طور قائم جهتگیری شود. سازه به صورت خطی و ارتجاعی قلمداد میشود. به علاوه، فرض میشود به سختی به زمین نگه داشته شوند، لذا اثرات برهمکنش خاک- سازه و انعطاف پذیری فنداسیون نادیده گرفته میشوند.
ABSTRACT Seismic Analysis of Asymmetric Buildings with Flexible Floor Diaphragms
Even though a rigid floor diaphragm is a good assumption for seismic analysis of most buildings, several building configurations may exhibit significant flexibility in floor diaphragm. However, the issue of static seismic analysis of such buildings for torsional provisions of codes has not been addressed in the literature. Besides, the concept of center of rigidity needs to be formulated for buildings with flexible floor diaphragms. In this paper, the definition of center of rigidity for rigid floor diaphragm buildings has been extended to unsymmetrical buildings with flexible floors. A superposition-based analysis procedure is proposed to implement code-specified torsional provisions for buildings with flexible floor diaphragms. The procedure suggested considers amplification of static eccentricity as well as accidental eccentricity. The proposed approach is applicable to orthogonal as well as nonorthogonal unsymmetrical buildings and accounts for all possible definitions of center of rigidity.
Introduction
Buildings are seldom, if ever, perfectly symmetric and frequently building vibrations involve coupling of lateral and torsional motion ~torsional coupling!. Besides the static eccentricity (es j) @defined as the distance between the center of mass ~CM! and the center of rigidity ~CR! at respective floors#, codes often require the designer to incorporate accidental eccentricity. Accidental eccentricity accounts for factors such as the rotational component of ground motion about the vertical axis, the difference between computed and actual values of the mass, stiffness or yield strength, and an unfavorable distribution of live load mass. Codal provisions on torsion differ significantly. However, the provisions of most codes for design eccentricity ed j at the j-th floor for static analysis of buildings can be expressed in the following general form: 
- مقاله درمورد تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- پروژه دانشجویی تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای منعطف
- پایان نامه در مورد تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- تحقیق درباره تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- مقاله دانشجویی تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر در قالب پاياننامه
- پروپوزال در مورد تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- گزارش سمینار در مورد تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر
- گزارش کارورزی درباره تحلیل زلزله ساختمان های نامتقارن با دیافراگم طبقه ای انعطاف پذیر