کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر

27,200 تومانشناسه فایل: 8815
- حجم فایل ورد: 756.7KB حجم پیدیاف: 280.3KB
- فرمت: فایل Word قابل ویرایش و پرینت (DOCx)
- تعداد صفحات فارسی: 32 انگلیسی: 12
- دانشگاه:School of Engineering, University of Warwick, Coventry, CV4 7AL, UK
- ژورنال: Computers and Operations Research (2)
مقدمه مقاله
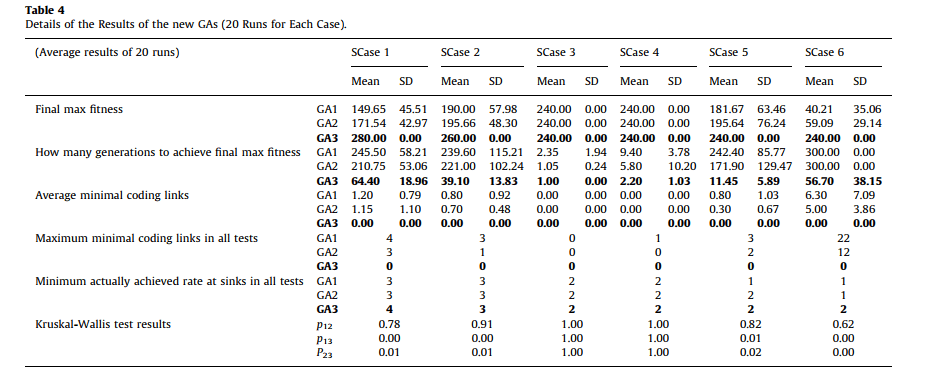
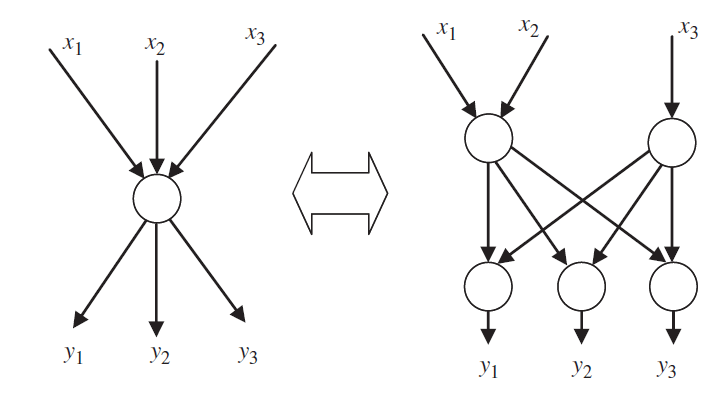
مفهوم برنامه نویسی در سطح بسته (پاکت)- که معمولا برنامه نویسی شبکه ای نامیده می شود- تمایل زیادی را از زمان انتشار [1] به خود جلب نموده است،که استفاده ی آن را برای چند قالب ها در شبکه های پاکت بی سیم نشان داده است.اکنون تایید شده است ،ممکن است برنامه نویسی شبکه ای به شدت عملکرد اجرایی شبکه را بر حسب توان عملیاتی (کار) شبکه ارتقا بخشد.لازم به ذکر است،بهینه سازی مرسوم شبکه ای در صدد به حداکثر رساندن جریان اطلاعات است که از طریق استفاده از ظرفیت زیاد لینک تا حد ممکن میسر می شود، در حالیکه برنامه نویسی شبکه ای با این فرضیه آغاز می شود که استفاده از ظرفیت کامل لینک تا کنون هر بار که ممکن بوده، بدست آمده است و از اینرو تلاش می شود توان عملیاتی شبکه در حفره ها با اجرای برنامه ها در ندها افزایش یابد.این مزیت برنامه نویسی شبکه ای می تواند در بافت نمونه ی نشان داده شده در شکل 1 الف و ب شناخته شود.در شکل 1 فرض می شود که دو بخش متفاوت از یک پاکت/ داده ی در اندازه ی واحد α و β، از ند منبع یک به ند حفره 6و 7 ارسال شده اند و ظرفیت هر لینکی فقط 1 است (در این مقاله ظرفیت لینک همانند بهینه سازی شبکه ای مرسوم تعریف می شود [1] و همه ی دیتاها در یک اندازه ی واحد هستند و همه ی لینک ها در ظرفیت واحد می باشند).هدف به حداکثر رساندن سرعت بدست آمده در هر حفره است یعنی میزان داده های مختلف دریافت شده از طریق یک حفره (sink) در یک بار.سرعت همچنین در واحدهای دیتا اندازه گیری می شود.از آنجایی که همه ی لینک ها در ظرفیت واحد هستند،ماکسیمم سرعت قابل دستیابی احتمالی در یک حفره با تعداد لینک های وارد شونده برابر است.با این وجود،لینک های مختلف ممکن است همان دیتا را حمل نمایند،همانند دو لینک وارد شونده ی ند 7 در شکل 1 الف و ازاینرو سرعتی که واقعا در هر حفره بدست آمده است، ممکن است از سرعت احتمالی کمتر باشد.این احتمالا موردی است که اگر ندها در شبکه فقط فروارد شوند و دیتایی که دریافت می کنند برگردانده شود.برای نمونه همانطور که در شکل 1 الف نشان داده شده است،ند حفره ی 7 می تواند فقط یک واحد دیتا β را در یک مرتبه دریافت نماید،گرچه ند 6 دیگر از طریق دریافت α و β به سرعت 2 می رسد .جریان اطلاعات در شکل 1 الف از نقطه نظر عادی ،مطلوب است زیرا هر لینکی یک واحد دیتا را حمل می کند،که یک استفاده ی کامل از ظرفیت لینک را ارائه می نماید.با این وجود، اگر ند 4 بتواند داده های دو لینک وارد شونده را از طریق عملیات “+” ترکیب نماید،آنگاه با استفاده از عملیات “-” دیتا دی کد (رمزگشایی) می شود،در یک سرعت 2 می تواند در هر دو حفره بدست آید،همانطور که در شکل 1 ب نشان داده شده است.لازم به ذکر است که نتیجه ی عملیات “+” مانند β+α در شکل 1 ب ،هم چنان یک عنصر دیتا در اندازه ی واحد است. از اینرو بدون فراتر رفتن از ظرفیت لینک
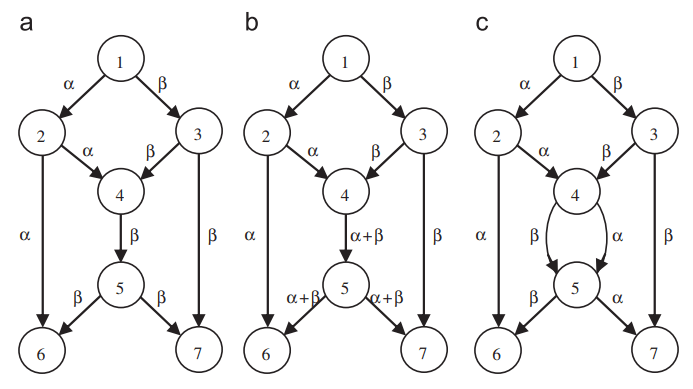
برنامه نویسی شبکه ،سرعت کل جریان اطلاعات را از طریق همان شبکه از 3 به 4 در شکل 1 افزایش می دهد که یک پیشرفت قابل توجه است.
گرچه کدینگ شبکه ممکن است در همه ی ندها در برخی از متون مربوطه مجاز تلقی شود،اما یک مشاهده ی جالب این است که یک سرعت هدف داده شده اغلب می تواند با اجرای کدینگ شبکه در فقط یک نسبت تقریبا کوچک از ندها بدست آید [2]. برای نمونه، در شبکه داده شده در شکل 1 ث ،کدینگ شبکه در هر دو ند 4 و 5 هیچ تفاوتی را بر حسب سرعت بدست امده در حفره ها ایجاد نخواهد کرد یا به بیان دیگر، کدینگ شبکه در آن شبکه لازم نیست.بنابراین یک سوال بوجود می آید:کدینگ شبکه در چه ندهایی نیاز به اجرا دارد یا چطور می توان بیشترین ظرفیت شبکه را در یک هزینه ی حداقل بر حسب منابع کدینگ شبکه ایجاد نمود؟ برای پاسخ به این سوال،یک مجموعه ی حداقل از ندها لازم است برای کدینگ یافت شود و این ثابت شده است که باید یک مسئله ی سخت NP باشد [3].در این مقاله، مسئله ی فوق یعنی به حداقل رساندن منابع کدگذاری شبکه به عنوان مسئله ی کدینگ شبکه (NCP) مطرح می شود.برخی از تلاش ها تا کنون با استفاده از متدهای مختلف صورت گرفته است تا این مسئله را بررسی نماید.برای نمونه دو دستاورد کمینه (حداقلی) در [5،4] گزارش شده است که مجموعه ی کمینه ی ندها را برای کدینگ شبکه اثبات نموده است تا یک سرعت هدف داده شده را بدست آورد.در [4] مشخص شده است که کدینگ در بیشتر از d-1 ند در شبکه های ناچرخه ای با دو منبع سرعت واحد و حفره های d لازم نیست.یک ح (کران) بالا بر روی تعدادی از ندها برای هم شبکه های ناچرخه ای و هم چرخه ای که از [5] بدست آمده بود،لازم بود.با این وجود،دستاورد های موجود در [5،4] مجموعه ی کمینه ی ندها را برای کد گذاری از طریق از بین بردن لینک ها در یک حالت اشباع نشدنی را مشخص می کند.
همانند تحقیق اتفاقی موازی در مقایس بزرگ و الگوریتم های بهینه سازی ، الگوریتم های ژنتیک (GAs) دارای منشا خوبی در حل مسائل سخت NP گوناگون هستند [8،7]،من جمله بهینه سازی کدینگ شبکه ای و تخصیص منابع [10،9].با این حال،بهینه سازی کدینگ شبکه ،نسبتا حوزه ی جدیدی برای GAs است و نتایج خیلی کمی در [2,11–13] گزارش شده است.نخستین تلاش برای به کارگیری GAs در کدینگ شبکه توسط کیم و همکارانش صورت گرفت [2].این آنگاه از شبکه های ناچرخه ای به شبکه های چرخه ای توسعه یافت و از موارد متمرکز به موارد نامتمرکز سوق یافت [11].نمایش ژنتیکی تاکید خاصی در کار بعدی داشت [12]،که از طریق پروپوزال یک الگوریتم توزیع شده برای بهبود اثر بخشی محاسباتی GA دنبال شد [13].
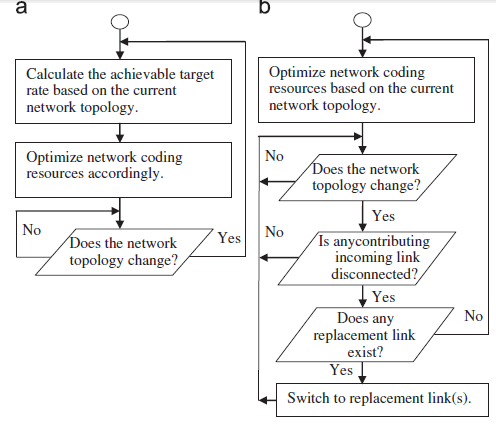
یک فرضیه ی مشترک در کار بهینه سازی کدینگ شبکه وجود دارد بنابراین سرعت هدف همیشه قابل دستیابی است اگر کدینگ در همه ی ندها مجاز باشد، و اجازه دهد توجه بر روی به حداقل رسانی تعداد لینک ها و ندهای کدینگ معطوف باشد.علی رغم این، د محیط های پویا (دینامیکی) همانند شبکه های بی سیم،کاملا این امکان وجود دارد که سرعت هدف ممکن است با توجه به عدم قطعیت در اتصالات بین ندها غیر قابل دستیابی باشد [14].اگر این اتفاق بیفتد، در واقع این سرعت است که به دست می آید نه سرعت هدف،که نقش مهم تری را در کدینگ شبکه ایفا می کند.مطالعات قبلی با استفاده از این فرضیه است که سرعت هدف قابل دستیابی است همانند [13-4،2] ،و این مسئله را در نظر نمیگیرد که سرعت واقعا در زمانی که منابع به حداقل می رسد بدست می آید و از اینرو به شدت به NCP (SNCP) محدود می شود.آنها ممکن است فقط برای NCP (DNCP) به کار رود که از طریق محاسبه ی مجدد سرعت هدف است و از اینرو منابع هر بار که تغییری در توپولوژی شبکه روی می دهد بهینه سازی می شوند.
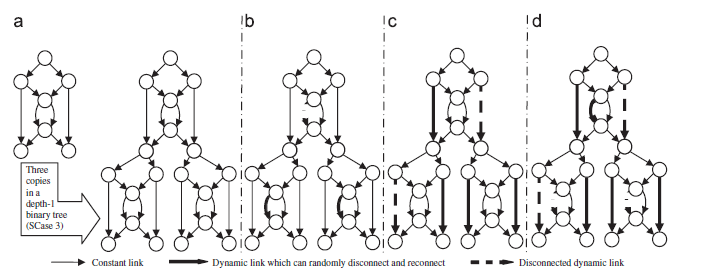
کدینگ شبکه در محیط های دینامیکی یک موضوع تحقیقاتی چالش برانگیز است.کدگذاری تصادفی شبکه ثابت شده است در بررسی تغییرات توپولوژی شبکه بسیار برجسته است زیرا به دانش توپولوژی کامل شبکه نیازی ندارد [19-15].با این وجود، در این مطالعات کدگذاری تصادفی شبکه ای، به حداقل رساندن منابع کدگذاری دغدغه ی ما محسوب نمی شود وهر ندی باید با بارهای (سنگینی) کدینگ خود در کل شبکه در ارتباط باشد یعنی کل ظرفیت شبکه برای انتقال سیگنال های ارسال شده از طریق منبع لازم نیست در دسترس باشند.بنابراین در حالیکه مزایای کدگذاری تصادفی شبکه باید تایید شود،اما باز هم لازم است شیوه ی بهبود کدگذاری شبکه ای بر اساس کل توپولوژی شبکه مورد تحقیق و بررسی قرار گیرد.قدرت در برابر تغییرات در توپولوژی شبکه یک مسئله ی خاص خواهد بود. همانطور که در بخش 3 توضیح داده خواهد شد، مدل DNCP که در این مقاله ارائه شده است چنین قدرتی را تا حدی نشان می دهد در زمانی که با کار قبلی مقایسه می شود [11،2].
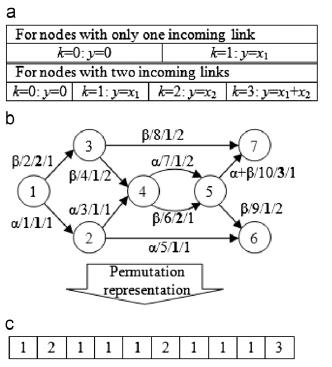
در مطالعه ی قبلی مان [20]،نتایج مقدماتی مربوط به طراحی GAs موثر برای به حداقل رساندن منابع کدینگ در NCP ،به ویژه درDNCP ،گزارش شده بودند اما کار به NCP محدود می شد که فقط از ساده ترین کدینگ افزودن (یعنی اندازه میدان 2 است) بین دو سیگنال وارد شونده استفاده می کرد.کار ارائه شده در این مقاله به پیشرفت های بیشتر نتایج قبلی ما از طریق گسترش کارمان به NCP مربوط میشود که در آنجا کدینگ با هر اندازه ی میدان معینی برای ترکیب هر تعداد مشخص از سیگنال وارد شونده تطبیق داده می شود.
ABSTRACT An effective genetic algorithm for network coding
The network coding problem (NCP), which aims to minimize network coding resources such as nodes and links, is a relatively new application of genetic algorithms (GAs) and hence little work has so far been reported in this area. Most of the existing literature on NCP has concentrated primarily on the static network coding problem (SNCP). There is a common assumption in work to date that a target rate is always achievable at every sink as long as coding is allowed at all nodes. In most real-world networks, such as wireless networks, any link could be disconnected at any time. This implies that every time a change occurs in the network topology, a new target rate must be determined. The SNCP software implementation then has to be re-run to try to optimize the coding based on the new target rate. In contrast, the GA proposed in this paper is designed with the dynamic network coding problem (DNCP) as the major concern. To this end, a more general formulation of the NCP is described. The new NCP model considers not only the minimization of network coding resources but also the maximization of the rate actually achieved at sinks. This is particularly important to the DNCP, where the target rate may become unachievable due to network topology changes. Based on the new NCP model, an effective GA is designed by integrating selected new problem-specific heuristic rules into the evolutionary process in order to better diversify chromosomes. In dynamic environments, the new GA does not need to recalculate target rate and also exhibits some degree of robustness against network topology changes. Comparative experiments on both SNCP and DNCP illustrate the effectiveness of our new model and algorithm.
Introduction
The notion of coding at the packet level –commonly called network coding –has attracted significant interest since the publication of [1], which showed its utility for multicast in wireline packet networks. It is now established that network coding may significantly improve network performance in terms of network throughput. It should be noted that conventional network optimization aims to maximize information flow by utilizing as much link capacity as possible, whilst network coding begins with the assumption that full link capacity utilization has already been achieved wherever possible and then attempts to further increase the network throughput at sinks by performing coding at nodes.
This advantage of network coding can be understood in the context of the example shown in Fig. 1.(a) and (b). It is assumed in Fig. 1 that two different pieces of one-unit-sized data/packets, a and b, are to be sent from the source node 1 to the sink node 6 and 7, and the capacity of every link is just 1 (in this paper, the link capacity is defined as the same as the one in conventional network optimization [1], all data are one-unit-sized, and all links are of unit-capacity). The aim is to maximize the rate achieved at each sink, i.e., the amount of different data received by a sink at one time. The rate is also measured in data units. Since all links are of unit-capacity, the potential maximal achievable rate at a sink is equivalent to the number of its incoming links. However, different links may carry the same data, such as the two incoming links of node 7 in Fig. 1.(a) and so the actually achieved rate at a sink may be less than the potential rate. This is likely to be the case if the nodes in the network only forward and replicate the data they receive. For example, as illustrated in Fig. 1(a), the sink node 7 can only receive 1 unit of data β at one time, although the other sink node 6 achieves a rate of 2 by receiving both α and β. The information flow in Fig. 1(a) is optimal from the conventional point of view because every link carries one unit of data, which gives a full utilization of the link capacity. However, if node 4 can combine data from its two incoming links through the ‘‘þ’’ operation, then by using the ‘‘–’’ operation to decode data, a rate of 2 can be achieved at both sinks, as shown in Fig. 1.(b). It should be noted that the result of operation ‘‘þ’’, e.g., α+β in Fig. 1.(b), is still an one-unit-sized data element. Therefore, without exceeding the link capacity, network coding increases the total rate of information flow through the same network from 3 to 4 in Fig. 1, a significant improvement.
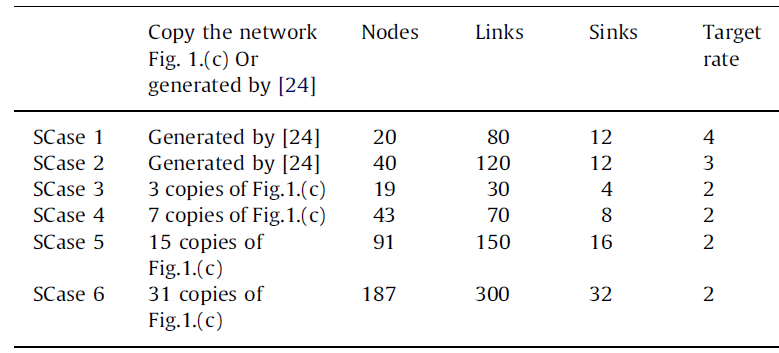
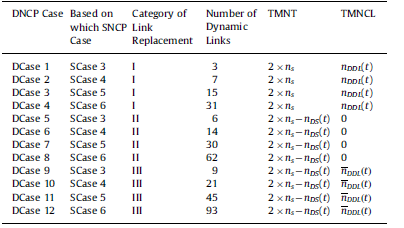
Although network coding may be allowed at all nodes in some of the relevant literature, an interesting observation is that a given target rate can often be achieved by conducting network coding at only a relatively small proportion of the nodes [2]. For instance, in the network given by Fig. 1(c), network coding at both nodes 4 and 5 will make no difference in terms of the rate achieved at the sinks or in other word, network coding is not necessary in that network. Therefore, a question is raised: at which nodes does network coding need to be conducted, or how does one make most of network capacity at a minimal cost in terms of network coding resources? To answer this question, a minimal set of nodes needs to be found for coding, and this has been proved to be an NP-hard problem [3]. In this paper, the above problem of minimizing network coding resources is referred to as the Network Coding Problem (NCP). Some attempts have already been made using different methods to address this problem. For instance, two minimal approaches were reported in [4,5] which ascertain the minimal set of nodes for network coding in order to achieve a given target rate. It was determined in [4] that coding is required at no more than d-1 nodes in acyclic networks with 2 unit-rate sources and d sinks. An upper bound on the number of nodes required for both acyclic and cyclic networks was derived in [5]. However, the approaches in both [4,5] determine the minimal set of nodes for coding by removing links in a greedy fashion. A linear programming method was reported in [6] to optimize the various resources used for network coding, and its optimal formulations involved a number of variables and constraints that grow exponentially with the number of sinks.
As large-scale parallel stochastic search and optimization algorithms, genetic algorithms (GAs) have a good provenance in the resolution of diverse NP-hard problems [7,8], including network optimization and resource assignment [9,10]. However, the optimization of network coding is a relatively new area for GAs, and very few results have been reported [2,11–13] to date. The first attempt to apply GAs to network coding was made by Kim et al. [2]. This was then extended from acyclic networks to cyclic networks and from centralized cases to decentralized cases [11]. The genetic representation was the particular focus in later work [12], followed by the proposal of a distributed algorithm to improve GA computational efficiency [13].
There is a common assumption in the network coding optimization work to date that the target rate is always achievable if coding is allowed at all nodes, permitting attention to be focused on the minimization of the number of coding links/nodes. However, in dynamic environments, such as wireless networks, it is quite possible that the target rate may become unachievable due to uncertainty in the connections between the nodes [14]. If this is the case, it is the rate that is actually achieved rather than the target rate that plays a more important role in network coding. The previous studies using the assumption that the target rate was achievable, such as [2,4–13], did not consider the rate actually achieved when minimizing resources, and were therefore largely limited to the static NCP (SNCP). They may only be applied to the dynamic NCP (DNCP) by calculating the target rate and then reoptimizing resources every time a change occurs in the network topology.
Network coding in dynamic environments is a challenging research topic. Random network coding has proved to be very promising in coping with network topology changes, as it does not require the knowledge of the entire network topology [15–19].
However, in these random network coding studies the minimization of coding resources is not a concern and each node has to communicate its coding weights throughout the network, which means that not all of the network capacity will be available to transmit the signals sent by the source. Therefore, whilst the advantages of random network coding should be acknowledged, it is still necessary to investigate how to improve network coding based on the entire network topology. Robustness against changes in network topology will be a particular concern. As will be explained in Section 3, the DNCP model proposed in this paper exhibits such robustness to some extent when compared with previous work [2,11].
In our previous study [20], preliminary results relating to the design of effective GAs for the minimization of coding resources in the NCP, particularly in the DNCP, were reported but the work was restricted to the NCP utilizing only the simplest addition coding (i.e., the field size is 2) between two incoming signals. The work presented in this paper is concerned with further developments of our previous results by extending our work to NCP where coding with any finite field size is adopted to combine any finite number of incoming signals.

- مقاله درمورد کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- برنامه نویسی شبکه (NCP) با الگوریتم موثر ژنتیک (GA)
- الگوریتم ژنتیک اثرگذار برای کدینگ شبکه
- پروژه دانشجویی کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- برنامه نویسی شبکه با الگوریتم ژنتیک
- پایان نامه در مورد کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- تحقیق درباره کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- مقاله دانشجویی کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر در قالب پاياننامه
- پروپوزال در مورد کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- گزارش سمینار در مورد کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر
- گزارش کارورزی درباره کدینگ شبکه (NC) با الگوریتم ژنتیک (GA) موثر