حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده

28,900 تومانشناسه فایل: 6496
- حجم فایل ورد: 681.7KB حجم پیدیاف: 645.9KB
- فرمت: فایل Word قابل ویرایش و پرینت (DOCx)
- تعداد صفحات فارسی: 25 انگلیسی: 12
- دانشگاه:
- Malek Ashtar University of Technology, Department of Electrical Engineering, Lavizan, Tehran, Iran
- Shahid Beheshti University, Department of Aerospace, Tehran, Iran
- ژورنال: ISA Transactions (1)
مقدمه مقاله
تجهیزات نوری (مانند IR، رادار، لیزر، و تلویزیون) دارای استفاده گسترده ای در بسیاری از کاربردها، همچون پردازش، موشکهای هدایت شونده، سیستمهای ردیابی و سیستمهای ناوبری، میباشد. در چنین سیستمهائی، محور حسگر نوری باید به دقت از پایگاه متحرک به یک هدف در حال حرکت یا ثابت شده نقطه گذاری شود. بنابراین، خط حسگر دید (LOS) بایست به شدت کنترل شود. در چنین محیطی که در آن تجهیزات در یک پلتفرم قابل حرکت نصب میشود، نگهداری جهت حسگر به سمت یک هدف چالشی جدی تلقی میشود.
پلتفرم تثبیت اینرسیایی (ISP) روش مناسبی برای حل این چالش است [1]. معمولا، سیستم طوقه دو محوره به منظور ارائه تثبیت سازی برای حسگر در زمان اثرگذاری اختلالات (آشوبهای) مختلف در آن مورد استفاده قرار میگیرد. مهمترین منابع آشوب تحرک زاویه دار پایگاه، دینامیکهای سیستم حلقوی، و عدم تعادل حجم طوقه میباشد. بنابراین الزامی است تا تمامی دینامیکهای نیروگاه به دست آید و نیروگاه بصورت تحلیلی قبل از طراحی مونتاژ طوقهای گرفته شود [2].
عملکرد سیستم به شدت به دقت مدلسازی نیروگاه بستگی دارد. یک نیروگاه معمول برای چنین مسائلی شامل یک مونتاژ طوقه الکترومکانیکی دارای آزادی زاویه دار در حسگرهای یک، دو یا سه محوره و یک یا چند حسگر الکترو نوری میباشد [3]. کنترل چنین سیستمهای تثبیت اینرسیایی LOS به دلیل کوپلینگهای عبوری بین شبکه های مختلف مسئله ساده ای نیست. علاوه بر این، این سیستمها مستلزم حفظ عملیات پایدار هستند و این که دقت نقطه گذاری و ردیابی برای هدف حتی در زمان وجود تغییرات در دینامیکهای سیستم و شرایط عملیاتی تضمین شود. در بسیاری از تحقیقات مدل ریاضیاتی و سیستم کنترل از سیستم طوقه دو محوره مطالعه شده است. چندین تغییر با استفاده از فرضیات مختلف ارائه شده است.
در [4]، روابط کوپلینگ هندسی و علم حرکتی با دو درجه از مونتاژ طوقه برای یک مورد ساده سازی به دست می آید در حالی که هر طوقه متعادل سازی می شود و بدنه های عناصر حلقهای شده درباره محورهای اصلی معلق هستند. [5] معادلات حرکت برای تنظیمات طوقه دو محوره را ارائه میکند، با فرض بر این که طوقه بدن های سفت و سختی دارند و دارای هیچ نوع عدم تعادلی در حجم نیستند.
در [5]، اکسراند نشان میدهد که آشوبهای تعادل با موقعیتهای تقارن اینرسیایی مخصوص حذف میشود، و انتخابهای مشخص از پارامترهای اینرسیایی میتواند کوپلینگ عبور اینرسیایی بین شبکه های سیستم طوقهای را حذف نماید. درجه مستقلی از آزادی عملیات طوقهای در یک محیط ارتعاش پیچیده توسط دانیل در [6] نشان داده میشود. وی نشان میدهد که چگونه ارتعاشات هر دو گشتاور آشوب عدم تعادل دینامیکی و استاتیکی را تهییج میکند که به صورت استاتیکی و دینامیکی با موازنه طوقه حذف میشود که این زمانبر است و مقرون به صرفه نیست [6]. در [7]، معادلات حرکت با این فرضیات ایجاد میشوند که دارای هیچ گونه عدم تعادل حجم دینامیکی نیستند و بدون برجسته سازی تاثیرات شتابهای زاویه های پایه هستند.
در [8]، مکانیزم طوقه دو محوره معرفی میشود و تنها مدلسازی محور آزیموت مورد تمرکز قرار میگیرد در حالی که زاویه مرتفع ثابت نگه داشته می شود و لحظات عبوری اینرسی صفر در نظر گرفته میشود. هم در [5] و هم در [9]، مدل دینامیکی طوقه های دینامیکی و مرتفع در فرضیاتی ایجاد می شوند که توزیع حجم طوقه ها متقارن است از اینرو تولیدات اینرسیا مورد غفلت قرار می گیرند و مدل ساده سازی میشود.
باید ذکر شود، که بیشتر این تحقیقات در نظر میگیرند که شبکههای آزیموت و مرتفع یکسان هستند بنابراین محور واحد شبیه سازی و تست میشود. بنابراین، کوپلینگ عبوری، که ناشی از حرکت زاویه دار پایگاه و خواص دینامیکهای سیستم طوقه میباشد، مورد چشم پوشی قرار میگیرد. همچنین، فرض میشود که توزیع حجم طوقه ها متقارن است پس طوقه ها هیچ عدم تعادل دینامیکی ندارند.
علاوه بر این، قانون نیوتن برای ایجاد مدل ریاضیاتی به کار گرفته میشود. از یک سو، سیستم کنترل تنظیمات طوقه دو محوره با استفاده از روشهای کنترل مختلف ایجاد میشود. در [7]، مد کشوئی مبتنی بر پروکسی در سیستم طوقه دو محوره به کار گرفته میشود؛ همچنین [10] کنترل مد کشوئی تحت مفروض شبکههای آزیموت و مرتفع یکنواخت جفت نشده را ارائه میکند. در [11]، ابزارهای سنتز مدرن همچون رگولاتور درجه دوم خطی (LQR) یا گاوسی درجه دوم خطی با کنترل بازیابی انتقال حلقه (LQG/LTR) برای یک کنترلر باند گسترده نیز در خط دید تثبیت سازی برای وسایل نقلیه زمینی متحرک مورد استفاده قرار میگیرد. همچنین [12] الگوریتم گاوسی درجه دوم خطی (LQG) برای برآورد و جبران سازی در زمان واقعی یک کلاس مخصوصی از آشوبها را ارائه میکند. همچنین روشهای کنترل معمول، برخی تکنیکهای کنترل پیشرفته همچون کنترل شدید و قوی [13]، کنترل ساختار متغیر (VSC) [14]، و متدولوژی کنترل [15] نیز در سیستمهای تثبیت اینرسیایی LOS به کار گرفته میشوند.
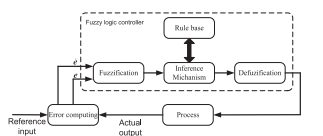
با این حال، اکثریت این الگوریتم ها پیچیده هستند و تشخیص آنها کار سختی میباشد. در سالهای اخیر، فناوری کنترل فازی بطور موفقیت آمیزی توسعه یافته است. این عملکرد سیستم کنترل را بهبود میبخشد، و دارای انطباق پذیری خوبی برای سیستم با عوامل نامشخص و مدل ریاضیاتی غیرخطی است [16، 17]. برخلاف کنترل معمولی، کنترل منطق فازی معمولا نیازی به مدل ریاضیاتی دقیق از فرایند ندارد که میبایست کنترل شود و همچنین منطق فازی یکی از بهترین حلها برای بخش گسترده از چالش مسائل کنترل و لجوج را در نظر میگیرد [18، 19].
دو نوع کنترل مبتنی بر منطق فازی؛ مبتنی بر سوگنو تاکاگی (T-S) و مبتنی بر ممدانی، وجود دارد. در آزمایشگاه مشاهده میشود که تقریبا تمامی سیستمهای دینامیکی غیر خطی توسط مدلهای فازی سوگنو تاکاگی با دقت زیادی نشان داده میشوند. در واقع، این تائید میکند که مدلهای فازی تاگاکی سوگنو تقریب سازهای غیر جهانی از هر سیستم غیر خطی همواری میباشند [20]. زمانی که سیستم منطق فازی درون طرح کنترل تطبیقی ترکیب میشود، کنترلر تطبیقی فازی پایدار به دست آمده در محیطهای پیچیده استفاده میشود که اختلالات را در پارامترهای نیروگاه تحمیل میکنند. در چنین محیط های، این کنترلر بصورت آنلاین برای اصلاح و تنظیم خودکار پارامترهای کنترل مورد استفاده قرار میگیرد [17].
اساسا، کنترلرهای فازی تطبیقی برای سیستمهای غیر خطی MIMO و SISO ناشناخته توسعه می یابند اما آنها تنها در سیستمهای غیر خطی محدود میشوند که در آن حالتها اندازهگیری میشود [21]. سیستم کنترل فازی در [22] به منظور کنترل نسبت اینرسیایی LOS پیاده سازی می شود. [23] کنترلر منطق فازی تمام ماتریس بهینه برای خط دید آینه ژیروسکوپ پلتفرم تثبیت ساز را معرفی میکند. سیستم استنتاج فازی نورو تطبیقی (ANFIS) و کنترلر مبتنی بر منطق فازی در [19-24] برای سرعت کنترل موتور سروو DC ارائه میشود.
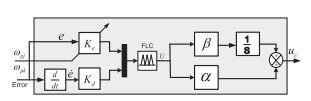
در [25]، مطالعه مقایسه ای از کنترلرهای ANFIS PID هیبریدی و، ANFIS، PID برای کنترل سرعت موتور جریان مستقیم بدون جاروب انجام میشود. در این مقاله، تکنیک فازی نوع PID خود تنظیم شونده برای سیستم طوقه دو محوره معرفی میشود که مدل ریاضیاتی آن بطور کامل با استفاده از معادلات لاگرانژ با در نظر گرفتن کوپلینگ چلیپائی بین دو شبکه، عدم تعادل دینامیکی، و شتاب های زاویه دار پایه، ایجاد میشود. اهداف کنترل عمدتا دستیابی به گذار خوب و عملکرد حالت پایدار با توجه به مرحله سفارشات ورودی است.
مشارکتهای این مقاله به شرح زیر خلاصه سازی میشود:
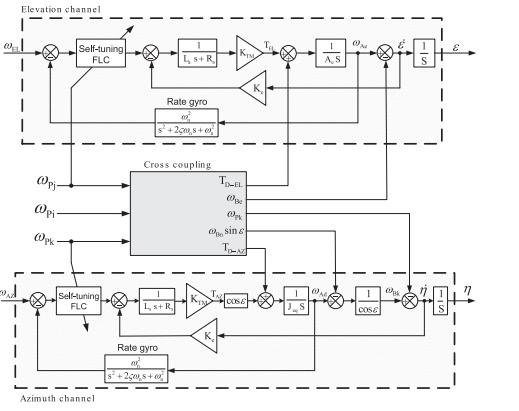
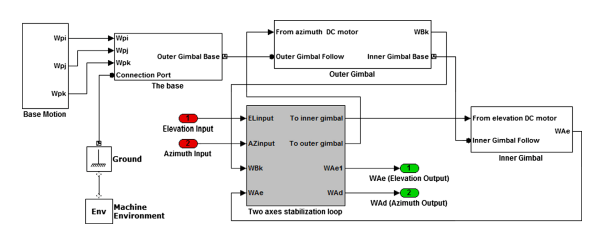
مدل کامل سیستم طوقه دو محوره با این فرض ایجاد می شود که طوقه ها دارای عدم تعادل حجم هستند و همچنین تمامی توزیعات اینرسیایی و کوپلینگ چلیپائی نیز در نظر گرفته میشود. پس، کنترلر فازی انطباقی قابل کاربرد با استفاده از الگوریتم تنظیم ساده طراحی میشود که بصورت قابل توجهی از حد خارج شدن بدون افزایش قابل توجه در مقدار زمان صعود را کاهش میدهد. مقاله به این حالت زیر سازماندهی میشود. در بخش 2، مسئله فرمول بندی میشود و معادلات حرکت طوقه ها در بخش 3 ایجاد میشود. پس از آن، حلقه پایاسازی ادغام و در بخش 4 ایجاد میشود. سپس، در بخش 5 کنترلر فازی ارائه شده طراحی میشود. نتایج شبیه سازی در بخش 6 معرفی میشود. در نهایت، یادآوری های نتیجه گیری در بخش 7 ارائه میشود.
ABSTRACT Stabilization loop of a two axes gimbal system using self-tuning PID type fuzzy controller
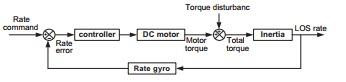
The application of inertial stabilization system is to stabilize the sensor’s line of sight toward a target by isolating the sensor from the disturbances induced by the operating environment. The aim of this paper is to present two axes gimbal system. The gimbals torque relationships are derived using Lagrange equation considering the base angular motion and dynamic mass unbalance. The stabilization loops are constructed with cross coupling unit utilizing proposed fuzzy PID type controller. The overall control system is simulated and validated using MATLAB. Then, the performance of proposed controller is evaluated comparing with conventional PI controller in terms of transient response analysis and quantitative study of error analysis. The simulation results obtained in different conditions prove the efficiency of the proposed fuzzy controller which offers a better response than the classical one, and improves further the transient and steady-state performance.
Introduction
The optical equipments (such as IR, radar, laser, and television) have found a wide use in many important applications, for example image processing, guided missiles, tracking systems, and navigation systems. In such systems, the optical sensor axis must be accurately pointed from a movable base to a fixed or moving target. Therefore, the sensor’s line of sight (LOS) must be strictly controlled. In such an environment where the equipment is typically mounted on a movable platform, maintaining sensor orientation toward a target is a serious challenge. An Inertial Stabilization Platform (ISP) is an appropriate way that can solve this challenge [1]. Usually, two axes gimbal system is used to provide stabilization to the sensor while different disturbances affect it. The most important disturbance sources are the base angular motion, the dynamics of gimballed system, and the gimbal mass unbalance. It is therefore necessary to capture all the dynamics of the plant and express the plant in analytical form before the design of gimbal assembly is taken up [2]. The system performance depends heavily on the accuracy of plant modelling. A typical plant for such problems consists of an electro-mechanical gimbal assembly having angular freedom in one, two or three axes and one or more electro-optical sensors [3]. The control of such LOS inertia stabilization systems is not a simple problem because of cross-couplings between the different channels. In addition, such systems are usually required to maintain stable operation and guarantee accurate pointing and tracking for the target even when there are changes in the system dynamics and operational conditions. The mathematical model and the control system of two axes gimbal system have been studied in many researches. Concerning the mathematical model, several derivations have been proposed using different assumptions. In [4], the kinematics and geometrical coupling relationships for two degree of freedom gimbal assembly have been obtained for a simplified case when each gimbal is balanced and the gimballed elements bodies are suspended about principal axes. [5] presented the equations of motion for two axes gimbal configuration, assuming that gimbals are rigid bodies and have no mass unbalance. In [5], Ekstrand has shown that inertia disturbances can be eliminated by certain inertia symmetry conditions, and certain choices of inertia parameters can eliminate the inertia cross couplings between gimbal system channels. A single degree of freedom gimbal operating in a complex vibration environment has been presented by Daniel in [6]. He illustrated how the vibrations excite both static and dynamic unbalance disturbance torques that can be eliminated by statically and dynamically balancing the gimbal which is regarded costly and time consuming [6]. In [7], the motion equations have been derived assuming that gimbals have no dynamic mass imbalance and without highlighting the effects of base angular velocities.
In [8], a two axes gimbal mechanism was introduced and just the modelling of azimuth axis was focused while the elevation angle was kept fixed and cross moments of inertia were taken to be zero. In both [5,9], the dynamical model of elevation and azimuth gimbals have been derived on the assumption that gimbals mass distribution is symmetrical so the products of inertia were neglected and the model was simplified. It must be mentioned, that most of these researches considered that the elevation and azimuth channels are identical so that one axis was simulated and tested. Therefore, the cross coupling, which is caused by base angular motion and the properties of gimbal system dynamics, was ignored. Also, it was supposed that gimbals mass distribution is symmetrical so the gimbals have not dynamic unbalance. In addition, Newton’s law has been utilized to derive the mathematical model. On the other hand, the control system of two axes gimbal configuration has been constructed using different control approaches. In [7], a proxy-based sliding mode has been applied on two axes gimbal system; also [10] proposed the sliding mode control under the assumption of uncoupled identical elevation and azimuth channels. In [11], modern synthesis tools such as linear quadratic regulator (LQR) or linear quadratic Gaussian with loop transfer recovery (LQG/LTR) control for a wideband controller have also been used in the line of sight stabilization for mobile land vehicle. Also, [12] presented a linear quadratic Gaussian (LQG) algorithm for estimating and compensating in real time a particular class of disturbances. Besides conventional control methods, some advance control techniques such as robust control [13], variable structure control (VSC) [14], and H1 control methodology [15] were also applied in LOS inertia stabilization systems. However, a majority of these algorithms were complex and difficult to be realized. In recent years, the fuzzy control technology has been developed successfully. It improves the control system performance, and has the good adaptability for the system with nonlinear mathematical model and uncertain factors [16,17]. Unlike the conventional control, the fuzzy logic control usually does not need the accurate mathematical model of the process which must be controlled and therefore fuzzy logic is considered one of the best solves for wide section of stubborn and challenging control problems [18,19]. There are two types of fuzzy logic-based controllers; Takagi Sugeno (T–S) based and Mamdani based. In literature, it can be found that almost all nonlinear dynamical systems can be represented by Takagi Sugeno fuzzy models to high degree of precision. In fact, it is proved that Takagi-Sugeno fuzzy models are universal approximators of any smooth nonlinear system [20]. When the fuzzy logic system is incorporated into adaptive control scheme, a stable fuzzy adaptive controller is obtained to be used in complex environments that impose perturbations on plant parameters. In such environments, this controller is used online to modify and adjust the control parameters automatically [17]. Basically, the adaptive fuzzy controllers have been developed for unknown SISO and MIMO nonlinear systems but they are limited only to nonlinear systems whose states can be measured [21]. A fuzzy control system was implemented in [22] to control inertial rate of LOS. [23] Introduced an efficient full-matrix fuzzy logic controller for a gyro mirror line-ofsight stabilization platform. A fuzzy logic based controller and adaptive-neuro fuzzy inference system (ANFIS) have been presented in [19–24] for speed control of DC servo motor. In [25], a comparative study of PID, ANFIS, and hybrid-PID ANFIS controllers has been accomplished for the speed control of brushless direct current motor. In this paper, a self-tuning PID-type fuzzy technique is introduced for a two axes gimbal system which its mathematical model is completely derived using Lagrange equation considering the cross coupling between two channels, the dynamic unbalance, and the base angular velocities. The control aims are mainly to achieve good transient and steady-state performance with respect to step input commands. The contributions of this paper can be summarized as follows. The complete model of two axes gimbal system is derived assuming that gimbals have mass unbalance as well as considering all inertia disturbances and cross coupling. Then, an applicable adaptive fuzzy controller is designed utilizing simple tuning algorithm which can considerably reduce the overshoot without significant increase in the rise time value. The paper is organized in the following manner. In Section 2, the problem is formulated and the equations of gimbals motion are derived in Section 3. Afterwards, the stabilization loop is investigated and constructed in Section 4. Then, in Section 5 the proposed fuzzy controller is designed. The simulation results are introduced in Section 6. Finally, the conclusion remarks are highlighted in Section 7.
- مقاله درمورد حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- حلقه تثبیت سیستم دوار دو محوره با استفاده از کنترل کننده فازی نوع PID خود تنظیم
- پروژه دانشجویی حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- کاربرد کنترل کننده فازی نوع PID در حلقه پایاسازی سیستم طوقه
- پایان نامه در مورد حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- تحقیق درباره حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- مقاله دانشجویی حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده در قالب پاياننامه
- پروپوزال در مورد حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- گزارش سمینار در مورد حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده
- گزارش کارورزی درباره حلقه تثبیت سیستم طوقه دو محوره به وسیله کنترل کننده فازی نوع PID خود تنظیم شونده