کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود

27,800 تومانشناسه فایل: 6287
- حجم فایل ورد: 1.2MB حجم پیدیاف: 885.4KB
- فرمت: فایل Word قابل ویرایش و پرینت (DOCx)
- تعداد صفحات فارسی: 33 انگلیسی: 24
- دانشگاه:Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran
- ژورنال: Journal of the Franklin Institute (1)
مقدمه مقاله
یکی از موضوعات ریاضی که بیش از سه قرن پیشینه دارد محاسبه های کسری است که میتوان آن را در کار های لیبنیز ، ریمن ، لیوویل ، گرونوالد ، و لتنیکوف نیز مشاهده کرد. با این وجود، این مبحث نتوانسته است در مدت های اخیر توجه زیادی را به خودش جلب کند، اما در سال های اخیر، به دلیل صحت بالای مدلسازی سیستم های فیزیکی با معادله های مرتبه ی کسری ، این سیستم ها دوباره در بسیاری از حوزه ها مانند فیزیک برای مدل سازی مورد استفاده قرار گرفته اند. همچنین در زمینه های مهندسی نیز بسیار کاربرد داشته است. در زمینه های میان رشته ای، سیستم های بسیار زیادی یافت شده است که میتوان آن ها را با معادله های کسری دیفرانسیل آن ها را نشان داد. به عنوان مثال، روند های الکتروشیمیایی، سیستم های ویسکوالاستیک، قطبیت دی الکتریک و موج های الکترومغناطیس ، و بعضی از سیستم های زیستی را میتوان در این دسته قرار داد. استفاده از امکانات نهان این محاسبه های کسری، برای بهبود عملکرد کنترل کننده های کلاسیک، یکی از جدید ترین امکانات این روش ریاضی میباشد.
یکی از پدیده هایی که به صورت مکرر در سیستم های غیر خطی مرتبه ی کسری دیده می شود پدیده های آشوبی میباشد. این سیستم های آشوبی یکی از طبقه های غالب سیستم های غیر خطی میباشند، که ویژکی های مختلفی دارند، مانند حساسیت پدیده به شرایط اولیه ی سیستم، جذب کننده های آشوبی، و حرکات فراکتال. مطالعه ی سیستم های آشوبی با مرتبه ی کسری یکی از جالب ترین حوزه های تحقیقاتی است. تا اکنون، محققان دینامیک غیر خطی مرتبه های کسری را در بسیاری از سیستم های آشوبی بررسی کرده اند، مانند سیستم های مرتبه کسری لورنز ، سیستم های روسلر مرتبه ی کسری، سیستم های مرتبه ی کسری چن ، سیستم های مرتبه کسری لو و سیستم های مرتبه کسری جنسیو – تسی و بعضی دیگر از سیستم های آشوبی. یکی ز جالب ترین زمینه ها در علوم غیر خطی که به صورت جامع در دهه های اخیر مورد بررسی قرار گرفته است کنترل شرایط آشوبی و همزمان سازی میباشد. ازین رو، بسیاری از روند های کنترل مانند کنترل حالت لغزشی ( SMC) ، کنترل خطی ، کنترل تطبیقی ، کنترل پسگام ، کنترل فعال، کنترل لغزشی حالت فازی، کنترل لغزشی تطبیقی ، و بعضی دیگر از روش ها به صورت موفق برای کنترل حالت های آشوبی و همزمان سازی مورد استفاده قرار گرفته است. روش های پس گام یک روش بازگشتی است که برای طراحی کنترل نوع خاصی از سیستم های دینامیک غیر خطی با استفاده از تابع های لیاپانوف به صورت موفق به روش سیستمی، طراحی شده است و میتواند پایداری سراسری با ردگیری خوب و عملکرد حالت گذار برای بیشتر سیستم های فیدبک دقیق پیشنهاد شده است. ازین رو، این موضوع یکی از روش های مهم و قوی برای سیستم های غیر خطی شده است. تکنیک های کنترل با حالت لغزش به عنوان یک برنامه ی قوی شناخته شده است تا بتوان کنترلی قوی برای سیستم های خطی و غیر خطی در سال های اخیر ، شناخته شود. برتری های محسوس SMC ، قوت آن نسبت به عدم قطعیت پارامتر ها و استحکام آن نسبت به اغتشاش های خارجی وجود دارد. این کنترل کننده یک روند قوی برای کنترل سیستم های دینامیک غیر خطی میباشد به خصوص برای سیستم های غیر قطعی. این موضوع به صورت گسترده مورد تحقیق قرار گرفته است و به دلیل عدم حساسیت نسبت به تغییر پارامتر های سیستم، اغتشاش های خارجی، پاسخ های گذرا و دینامیک سریع خوب بسیار کاربرد پیدا کرده است و برای استفاده در سیستم های مسئله های آشوبی بسیار مناسب است. در طرح های کنترلی ، برای اجرای یک سطح سوییچ مناسب و تضمین پایداری سیستم های SMC، یک تخمین خوب از کران های عدم قطعیت، شامل دینامیک غیر قطعی، تغییر پارامتر ها، و اغتشاش خارجی باید در خروجی طراحی وجود داشته باشد. ازین رو، در حالت عملی، این چنین کران هایی را نمیتوان به سادگی تخمین زد، بعضی از برنامه های ملاحظه کار کنترلی نیز در دسترس هستند تا باید برای پایداری سیستم حلقه بسته، اعمال شود.
به دلیل توانایی تخمین سراسری سیستم های فازی و شبکه های عصبی ، از این روش ها در مسئله های کنترل آشوبی به صورت گسترده استفاده شده است. اخیرا، توانایی های یادگیری شبکه های عصبی برای تحقق طراحی سیستم های فازی به عنوان یکی از قوی ترین روش ها شناسایی شده است. شبکه های عصبی فازی ( NFN) شامل معیار های یادگیری سطح پایین و توان محاسباتی شبکه های عصبی ، و یادگیری مانند انسان و منطق یابی نظریه ی فازی میباشد. اما، در شرایط پیچیده، که پارامتر های دستگاه سوژه ای به اغتشاش ها هستند و یا زمانی که دینامیک سیستم برای مدل های ریاضی و توصیف آن بسیار پیچیده باشند، طرح های تطبیقی باید به صورت آنلاین داده ها را جمع آوری کند و پارامتر های کنترلی را به صورت خودکار تنظیم کند.
اخیرا، بسیاری از نتایج محسوس با استفاده از تکنیک های هوشمند کنترل تطبیقی ترکیبی برای سیستم های آشوبی غیر قطعی به دست آمده است. برای سیستم های مرتبه ی کسری، این ایده تا حدی توسط نویسنده های مختلف در مقالات توسعه یافته است. به عنوان مثال در مرجع شماره ی 54 ، سیستم های مرتبه ی جزیی لیو از طریق روش حالت لغزشی مرتبه ی کسری با استفاده از سیستم های فازی کنترل میشود. در مرجع شماره ی 55 ، روش کنترل لغزشی فازی تطبیقی برای همزمان سازی سیستم های آشوبی مرتبه کسری غیر قطعی مورد استفاده قرار گرفته است که در این روش یک ترکیب لیاپانوف برای تنظیم کردن پارامتر های آزاد کنترل کننده ی فازی تطبیقی به صورت آنلاین توسط قانون کنترل فیدبک خروجی و قانون تطبیقی ، پیشنهاد شده است. همزمان سازی سیستم های آشوبی مرتبه ی کسری غیر قطعی از طریق کنترل حالت لغزشی فازی تطبیقی با وقفه ی زمانی نوع 2 در مرجع 56 در نظر گرفته شده است تا بتوان سطح بالایی از عدم قطعیت را که در سیستم های آشوبی مرتبه ی کسری دینامیک پیش روی کنترل کننده های منطقی فازی وجود دارد تا حل کند، مانند عدم قطعیت های موجود در ورودی FLC ها، عدم قطعیت در خروجی کنترل کننده، عدم قطعیت زبانی و عدم قطعیت موجود در داده های تمرینی نویز دار. در مرجع شماره ی 57 ، یک کنترل کننده ی حالت لغزشی تطبیقی فازی طراحی شد تا دو سیستم آشوبی مرتبه کسری با تاخیر زمانی را با هم هماهنگ کند که در این سیستم ها، سیستم های منطقی فازی با تاخیر زمانی تطبیقی ایجاد شده است تا تابع های نا مشخص مرتبه کسری با تاخیر زمانی را تخمین بزند. در مرجع شماره ی 58 ، طراحی کنترل کننده ی حالت لغزشی موجک های فازی تطبیقی برای سیستم های غیر خطی تطبیقی مورد مطالعه قرار گرفت تا طبقه ای از سیستم هایی با غیر خطی بودن بالا بررسی شود در حالی که ساختار این سیستم نا مشخص بود و دانش اولیه نسبت به عدم قطعیت در دسترس نبود. طرح پیشنهاد شده برای ایجاد شرایط معادل کنترل و یک کنترل کننده ی انتگرالی تناسبی ( API) برای اجرای شرایط سوییچ استفاده شده است تا بتوان ورودی کنترلی روانی را ایجاد کرد. در تلاش بعدی همین تی تلاش کرد تا سیستم های آشوبی آرنئودو و سیستم پاسخ آن را با تابع های غیر خطی نامشخص همزمان کنند. بر اساس روش پس گام، یک طرح کنترلی تطبیقی فازی با ترکیب سیستم منطقی فازی با پارامتر های آن ارائه شد تا بتوان همزمان سازی را به دست آورد. در مرجع شماره ی 60 ، یک کنترل کننده ی هوشمند تطبیقی مرتبه ی کسری بر اساس روش های کنترلی فعال طراحی شده است که در آن، کران های نامشخص عدم قطعیت فشرده از طریق یک تخمین زننده ی تطبیقی عصبی فازی ، تخمین زده شده است.
در این مقاله، برای ترکیب کردن ظرفیت های کنترل پس گام و کنترل حالت لغزشی، یک کنترل کننده ی حالت لغزشی پسگام هوشمند تطبیقی برای پایدار سازی سیستم های مرتبه کسری آشوبی در زمان محدود پیشنهاد شده است. این کنترل کننده ی عصبی فازی هوشمند برای تخمین زدن تابع های نامشخص استفاده شده است. استفاده از کنترل کننده های کمکی نیز برای بهبود سرعت و عملکرد سیستم پیشنهاد شده ی کنترلی استفاده شده است تا بتوان عدم قطعیت ها را کاهش داده، اغتشاش خارجی و خطای تخمین را کم کرد. این سه عامل به صورت نامشخص کران دار هستند و ازین رو، این کنترل کننده از قدرت طراحی های تطبیقی استفاده میکند. در طراحی قانون کنترل، پارامتر های شبکه ی عصبی فازی و تخمین زننده های کران های عدم قطعیت، تخمین زننده ی کران های اغتشاش های خارجی و خطای تخمین، بر اساس یک طرح تطبیقی تنظیم میشود. پایداری جانبی این کنترل کننده بر اساس نظریه ی لیاپانوف و زمان محدود برای سطح لغزش نیز اثبات شده است. نتایج نشان دهنده ی پایداری لیاپانوف در سیستم حلقه بسته ، قدرت نسبت به عدم قطعیت، اغتشاش های خارجی و تخمین خطا میباشد در حالی که سیگنال های این کنترل همچنان کران دار میباشد.
بقیه ی این مقاله نیز به صورت زیر سازمان یافته است : در بخش 2 ، تعاریف و بعضی از اصول اولیه ی محاسبه های کسری نیز معرفی میشود. بخش 3 نیز نشان دهنده ی مدل های دینامیک سیستم های آشوبی مرتبه کسری است که در این مقاله استفاده شده است و در بخش 4 توصیفی از ساختار شبکه های عصبی فازی ارائه شده است. توصیف های مسئله در بخش 5 توصیف شده است. شبیه سازی های عددی نیز نشان دهنده ی اعتبار و کارایی کنترل کننده های طراحی شده میباشد که در بخش 6 ارائه شده است. در نهایت، جمع بندی نیز در بخش 7 ارائه شده است.
ABSTRACT Finite-time fractional-order adaptive intelligent backstepping sliding mode control of uncertain fractional-order chaotic systems
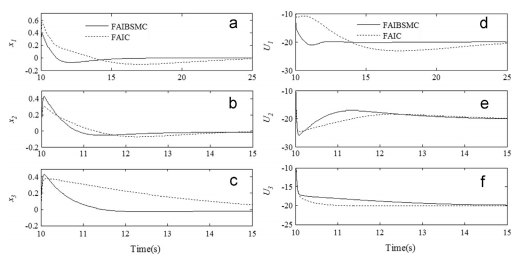
This paper precedes chaos control of fractional-order chaotic systems in presence of uncertainty and external disturbances. Based on some basic properties on fractional calculus and the stability theorems, we present a hybrid adaptive intelligent backstepping-sliding mode controller (FAIBSMC) for the finite-time control of such systems. The FAIBSMC is proposed based on the concept of active control technique. The asymptotic stability of the controller is shown based on Lyapunov theorem and the finite time reaching to the sliding surfaces is also proved. Illustrative and comparative examples and simulation results are given to confirm the effectiveness of the proposed procedure, which consent well with the analytical results.
Introduction
One of the mathematical topics with more than three centuries history is fractional calculus theory which can be traced back to Leibniz, Riemann, Liouville, Grünwald, and Letnikov [1–3]. Although, it did not attract much attention for a long time, but, in the recent years, due to high modeling accuracy of real physical systems by fractional order equations, these systems have been increasingly used for modeling in many areas such as physics [4] and engineering [5]. In interdisciplinary fields, many systems have been found which can be described by fractional differential equations. For instance, electrochemical processes [6], viscoelastic systems, dielectric polarization and electromagnetic waves [2,7], and some biological systems [8] can be encountered in this category. Applying latent possibilities of fractional calculus, in order to improve the performance of classical controllers, is one of the recent applications of this mathematical topic.
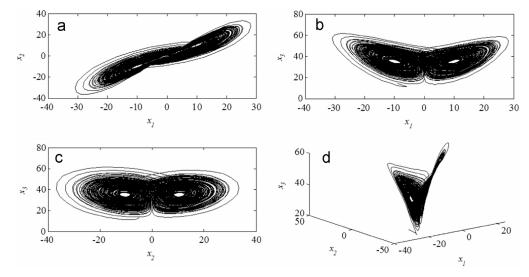
One of the phenomena which are frequently observed in the fractional order nonlinear systems is chaos phenomenon. Chaotic systems are a prominent class of nonlinear systems, which have various special properties, such as phenomenal sensitivity to system initial conditions, chaotic attractors, and fractal motions. Study of chaotic systems with fractional orders is one of the hottest research areas. Up to now, researchers have studied the fractional order nonlinear dynamics of many popular chaotic systems, such as fractional order Lorenz system [9–11], fractional order Rössler system [12,13], fractional order Chen system [12,14], fractional order Lü system [15,16] and fractional order Genesio-Tesi system [17] and some other chaotic systems. One of the most attractive topics in the nonlinear science which has been comprehensively studied in the recent decades is Chaos control and synchronization. Therefore, many control procedures such as sliding mode control (SMC) [18–22], linear control [23], adaptive control theory [24–26], backstepping control [27–30], active control [31], fuzzy sliding mode control [32], adaptive sliding mode control [33,34] and some other methods [35–38] have been successfully applied to chaos control and synchronization. Backstepping method is a recursive procedure which was proposed for designing controls for a special type of nonlinear dynamical systems by choosing Lyapunov functions skillfully and a systematic design approach, and it can guarantee global stability, good tracking and transient performance for most of strict-feedback systems. Therefore, it has become one of the important and popular approaches for nonlinear systems [39,40]. Sliding mode control technique has been known as a powerful strategy to design robust control for linear and nonlinear systems in recent years. The significant superiorities of SMC are its robustness to parameters uncertainty and its immutability to external disturbances. It is also a strong robust procedure for controlling the nonlinear dynamic systems [41–43], especially for uncertain systems. It has been studied extensively and received many applications due to its insensitivity to system parameter variations, external disturbances rejection, fast dynamic and good transient response which made it applicable for the control problem of chaotic system [18–22,32–34]. In this control scheme, for conducting an effective switching surface and guaranteeing the stability of an SMC system, a good estimation of the uncertainty bound, including the unknown dynamics, parameter variation, and external disturbance must be available at the outset of the design. Since, in practice, such bounds cannot be estimated easily, some conservative control strategies are also need to be applied for ensuring stability of the closed loop system.
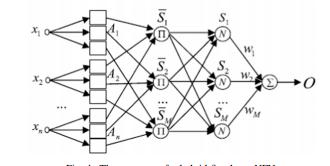
Due to the universal approximation ability of fuzzy systems and neural networks it has been widely used in chaos control problems [44–46]. Recently, the learning abilities of neural networks to realize to design of fuzzy systems have been recognized as a powerful approach [47]. The neuro-fuzzy-network (NFN) possesses the merits of low-level learning and computation power of neural networks, and the high-level human-like thinking and reasoning of fuzzy theory. However, in complicated situations, where plant parameters are subject to perturbations or when the dynamics of the systems are too complex for a mathematical model to describe, adaptive schemes should be used online to gather data and adjust the control parameters, automatically.
Recently, many significant results have been obtained by using hybrid adaptive intelligent control techniques for uncertain chaotic systems [48–53]. For fractional-order systems, this idea has been extended to some extent, by the researchers, in the literature. For example, in [54], uncertain fractional-order Liu system is controlled via fuzzy fractional-order sliding mode method. In [55], adaptive fuzzy sliding mode control has been employed for synchronization of uncertain fractional order chaotic systems, in which, a fuzzy Lyapunov synthesis approach is proposed to tune free parameters of the adaptive fuzzy controller on line by output feedback control law and adaptive law. Synchronization of uncertain fractional order chaotic systems via adaptive interval type-2 fuzzy sliding mode control was considered in [56] to handle high level uncertainties facing the fuzzy logic controller (FLC) in dynamic fractional order chaotic systems such as uncertainties in inputs to the FLC, uncertainties in control outputs, linguistic uncertainties and uncertainties associated with the noisy training data. In [57], an adaptive fuzzy sliding mode control was designed to synchronize two different uncertain fractional-order time-delay chaotic systems, where, the adaptive time-delay fuzzy-logic system is constructed to approximate the unknown fractional-order time-delay-system functions. In [58], the design of adaptive fuzzy wavelet neural sliding mode controller for uncertain nonlinear systems was studied for a class of high-order nonlinear systems while the structure of the system is unknown and no prior knowledge about uncertainty is available. The proposed scheme was employed to construct equivalent control term and an Adaptive Proportional-Integral (A-PI) controller for implementing switching term to provide smooth control input. Next attempt ([59]) deals with the synchronization for Arneodo chaotic system and response system with unknown nonlinear function. Based on backstepping method, a fuzzy adaptive control scheme by combining fuzzy logic system with parameter was presented to achieve synchronization. In [60], a fractionalorder adaptive intelligent controller was designed based active control method, in which, the unknown boundaries of the lumped uncertainties are estimated via an adaptive neuro-fuzzy approximator.
In this paper, in order to merge the capabilities of backstepping control and sliding mode control, an adaptive intelligent backstepping sliding mode controller is proposed for stabilization of fractional order chaotic systems in finite time. The intelligent neuro-fuzzy controller is used to estimate unknown functions. The use of auxiliary controller is in order to improve velocity and performance of the proposed control system and to dispel the uncertainties, external disturbances and error approximation. These three factors are unknown bounded, and so the controller will take advantage of robust adaptive design. In design of the control law, neuro-fuzzy network parameters and the uncertainties bound estimator, external disturbances bound estimator and approximation error, are adjusted as an adaptive scheme. The asymptotic stability of the controller is shown based on Lyapunov theorem and the finite reaching time to the sliding surfaces is also proved. The results are indicative of the Lyapunov stability of the closed loop system, robustness against uncertainties, external disturbances and approximation errors, while the control signal remains bounded.
The rest of this paper is organized as follows: In Section 2, the definitions and some basic properties of fractional calculus are introduced. Section 3, presents dynamic models of fractional order chaotic systems which are used in this paper and in Section 4 description of the neurofuzzy network structure is presented. Problem description is described in Section 5. Numerical simulation results which confirm the validity and feasibility of the designed controllers, are shown in Section 6. Finally, conclusions are given in Section 7.

- مقاله درمورد کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- کنترل حالت لغزشی پسگام هوشمند تطبیقی به صورت مرتبه کسری زمان محدود بر سیستم آشوبی مرتبه کسری نامعلوم
- پروژه دانشجویی کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- کنترل حالت لغزشی پس گام بر سیستم آشوبی مرتبه کسری نامعلوم
- پایان نامه در مورد کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- تحقیق درباره کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- مقاله دانشجویی کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود در قالب پاياننامه
- پروپوزال در مورد کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- گزارش سمینار در مورد کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود
- گزارش کارورزی درباره کنترل حالت پسگام لغزشی هوشمند تطبیقی بر سیستم آشوبی مرتبه کسری نامعلوم به صورت مرتبه کسری زمان محدود